正文

1. Softmax 的定义

softmax函数又称归一化指数函数，是基于 sigmoid 二分类函数在多分类任务上的推广；在多分类网络中，常用 Softmax 作为最后一层进行分类。

Softmax 的计算公式如下：

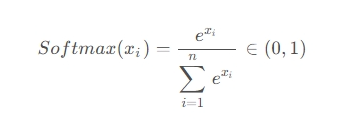
2. Softmax 使用 e 的幂次的作用

对比普通的 max() 方法，Softmax 的独特之处就是使用的 e 的幂函数，其目的是为了两极化：

Softmax 可以使正样本（正数）的结果趋近于 1，使负样本（负数）的结果趋近于 0；且样本的绝对值越大，两极化越明显。

2.1 代码验证

（1）先用 numpy 来验证一下：

import numpy as np

# 计算向量 x 的 softmax

def softmax(x: list) -> list:

    exps = np.exp(x)

    return list(exps / np.sum(exps))

if __name__ == '__main__':

    input = [-2, -1, 0, 1, 2]

    output = softmax(input)

    output = [float('{:.4f}'.format(i)) for i in output]

    print(f"{output}")

对比两组输入输出：

(1) input = [-0.5, -0.2, 0, 0.2, 0.5]     output = [0.1145, 0.1546, 0.1888, 0.2307, 0.3114]

(2) input = [-5,   -2,   0, 2,   5]       output = [0.0, 0.0009, 0.0064, 0.0471, 0.9456]

可以明显看到， x 的数值分布越不均匀，则 S o f t m a x ( x ) Softmax(x)Softmax(x) 的两极化越明显 在上面第二个 input 中， -5 对应的输出已经非常接近0，而 5 对应的输出已经接近 0.95

Softmax 可以使数值较大的值获得更大的概率

（2）再看看 PyTorch 中的 Softmax 函数：

import torch

import torch.nn as nn

input = torch.Tensor([-0.5, -0.2, 0, 0.2, 0.5])

softmax = nn.Softmax(dim=0)

output = softmax(input)

print(output)    # tensor([0.1145, 0.1546, 0.1888, 0.2307, 0.3114])

可以看到 PyTorch 的计算结果与我们自己用 numpy 算的是一致的。

2.2 数学原理分析

从数学原理上分析，是因为当 x 的数值分布越不均匀时，e m a x ( x i ) e^{max(x_i)}e 

max(x i)与 ∑ i = 1 n x i \displaystyle \sum^{n}_{i=1}{x_i} i=1∑n x i

  非常接近，导致 S o f t m a x ( m a x ( x i ) ) → 1 Softmax(max(x_i)) \rightarrow 1Softmax(max(x i ))→1 ，而 S o f t m a x ( m i n ( x i ) ) → 0 Softmax(min(x_i)) \rightarrow 0Softmax(min(xi))→0

3. 解决 Softmax 的数值溢出问题

3.1 什么是数值溢出？

数值溢出是 Softmax 函数经常遇到的问题，数值溢出包括数值上溢和下溢两张情况：

（1）上溢：数值较大的数据经过一些运算后其数值非常大，以至于超过计算机的存储范围而无法继续运算，在程序中表现为 NAN

（2）下溢：非常接近0 的数据被四舍五入为 0，从而产生毁灭性的舌入误差。

3.2 解决数值上溢问题：x i − m a x ( x ) x_i-max(x)xi−max(x)

由于 Softmax 中存在 e 的幂次，这将很容易导致数值溢出问题：

（1）当 x i → − ∞ x_i \rightarrow -\inftyxi→−∞时，S o f t m a x ( x ) Softmax(x)Softmax(x) 的分母将接近 0，导致 S o f t m a x ( x ) → 0 Softmax(x) \rightarrow 0Softmax(x)→0，会出现数值下溢问题。

（2）当 x i → + ∞ x_i \rightarrow +\inftyxi→+∞时，S o f t m a x ( x ) Softmax(x)Softmax(x) 的分子和分母都接近正无穷大，导致 S o f t m a x ( x ) Softmax(x)Softmax(x) 的结果是未定的。

依然首先通过代码来说明，可以看到：当输入数值较小时，Softmax 的输出为 0；而当输入数值较大时，Softmax 的输出为 nan

import numpy as np

# 计算向量 x 的 softmax

def softmax(x: list) -> list:

    exps = np.exp(x)

    return list(exps / np.sum(exps))

if __name__ == '__main__':

    input = [-1000, -200, 0, 200, 1000]

    output = softmax(input)

    print(f"{output}")     # [0.0, 0.0, 0.0, 0.0, nan]

上述两个问题可以通过公式 (2) 同时解决：

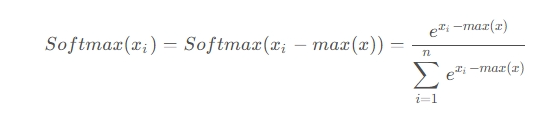
简单推导一下就知道，S o f t m a x ( x i ) = S o f t m a x ( x i − m a x ( x ) ) Softmax(x_i)=Softmax(x_i-max(x))Softmax(x 

i

 )=Softmax(x 

i

 −max(x)) 是成立的；因为 Softmax 的函数值不会因为输入向量减去或加上一个标量而改变（标量在分子和分母中会抵消）。

将 x i x_ix 

i

  减去 m a x ( x ) max(x)max(x) 使得 exp 指数的最大参数 x i − m a x ( x ) x_i-max(x)x 

i

 −max(x) 为 0 ，这避免了数值上溢的可能。同时，分母中有一项是固定的 e m a x ( x ) − m a x ( x ) = 1 e^{max(x)-max(x)} =1e 

max(x)−max(x)

 =1，这保证分母不会为 0 ，避免出现分母奇异的情况。但公式 (2) 并不能避免分子为 0 从而导致数值下溢的情况。

3.3 解决数值下溢问题：log_softmax

使用 x i − m a x ( x ) x_i-max(x)x 

i

 −max(x) 可以避免数值上溢，但不能完全解决数值下溢的问题。log_softmax 正是为了解决 softmax 中的数值下溢的情况；对公式(2)取对数得到 log_softmax 的表达式：

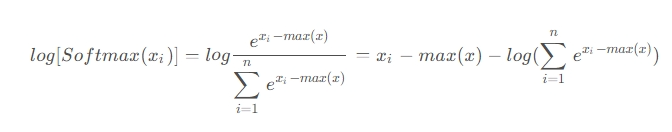
l o g [ S o f t m a x ( x i ) ]  中都是常数项，因此不会出现数值溢出问题。

4. PyTorch 中 CrossEntropyLoss 与 Softmax 的关系

PyTorch 中 CrossEntropyLoss 的接口是 torch.nn.CrossEntropyLoss()

先说结论1：

nn.CrossEntropyLoss() 中已经集成了 Softmax，因此如果使用nn.CrossEntropyLoss() 作为损失函数，则网络的最后一层不需要也不能加 Softmax 层

nn.CrossEntropyLoss() 的官方介绍为 torch.nn.CrossEntropyLoss()，其计算公式为：

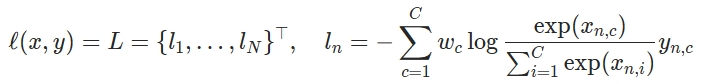
再说结论2：

nn.CrossEntropyLoss 是 nn.LogSoftmax 和 nn.NLLLoss 的组合

nn.LogSoftmax 就是 3.3 中讲的 log_softmax，nn.NLLLoss 其实就是先求和，再取负数。所以先做 LogSoftmax 再做 NLLLoss 其实就等价于直接做CrossEntropyLoss

使用 PyTorch 验证一下：

import torch

import torch.nn as nn

# 输入数据和 label

input = torch.Tensor([[-0.5, -0.2, 0, 0.2, 0.5]])

target = torch.tensor([0.35]).long()

log_softmax = nn.LogSoftmax(dim=1)

CEL = nn.CrossEntropyLoss()

NLL = nn.NLLLoss()

# CrossEntropyLoss

output_CEL = CEL(input, target)

print(f"output_CEL = {output_CEL}")

# LogSoftmax + NLLLoss

logSM_input = log_softmax(input)

output_NLL = NLL(logSM_input, target)

print(f"output_NLL = {output_NLL}")

"""

output_CEL = 2.1668357849121094

output_NLL = 2.1668357849121094

"""

可以看到，nn.CrossEntropyLoss 的计算结果与 nn.LogSoftmax + nn.NLLLoss 的组合计算结果完全相同。

本节参考资料：

Pytorch踩坑记之交叉熵（nn.CrossEntropy，nn.NLLLoss，nn.BCELoss的区别和使用）

Pytorch 中使用nn.CrossEntropyLoss的注意点（不需要额外的softmax）

原文地址

https://blog.csdn.net/qq_43799400/article/details/131202148?ops_request_misc=&request_id=&biz_id=102&utm_term=softmax&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-3-131202148.nonecase&spm=1018.2226.3001.4187